扩散模型（Diffusion models）

Beijing, China: 🌦 🌡️+32°C 🌬️←19km/h

🗒️ 写在前面

本文旨在对 扩散模型（Diffusion Model） 进行系统性概述，介绍其基本原理、核心流程以及与之相关的部分数学推导。通过对正向扩散过程（forward process）与逆向生成过程（reverse process）的解析，帮助读者建立对扩散模型工作机制的整体认识，并为后续深入理解其在图像生成、语音建模等任务中的应用打下基础。

GAN 模型因其对抗性训练性质，在训练过程中可能不稳定且生成的样本缺乏多样性。VAE 依赖于一个替代损失函数。Flow 模型需要采用专用架构来构建可逆变换。扩散模型受非平衡热力学启发，通过定义一个扩散步骤的马尔可夫链，逐步向数据中添加随机噪声，随后学习逆转扩散过程以从噪声中构建目标数据样本。与 VAE 或 Flow 模型不同，扩散模型采用固定流程进行学习，且潜在变量具有高维度（与原始数据相同）。

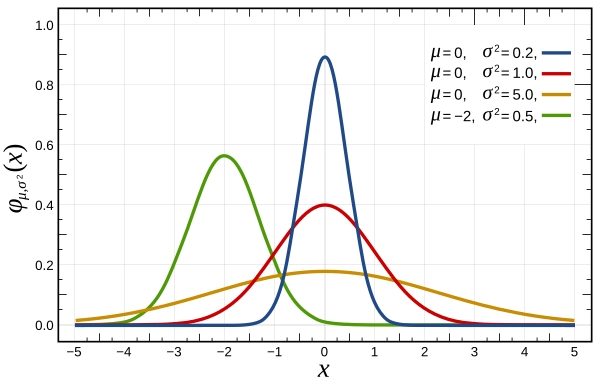
在开始教程之前，本文用了许多关于高斯分布（Gaussian distribution） 的函数的相关性质，先列在此处：

简写	中文	全称	公式
Notation	符号	Normal distribution	$\mathcal{N}(\mu, \sigma^2)$
Parameters	参数	Parameters: mean and variance	$\mu \in \mathbb{R}$ , $\sigma^2 \in \mathbb{R}_{>0}$
Support	支持集	Support of distribution	$x \in \mathbb{R}$
PDF	概率密度函数	Probability Density Function	$\frac{1}{\sqrt{2 \pi \sigma^2}} e^{-\frac{(x-\mu)^2}{2 \sigma^2}}$
CDF	累积分布函数	Cumulative Distribution Function	$\Phi\left(\frac{x-\mu}{\sigma}\right)=\frac{1}{2}\left[1+\operatorname{erf}\left(\frac{x-\mu}{\sigma \sqrt{2}}\right)\right]$
Quantile	分位数	Quantile function	$\mu+\sigma \sqrt{2} \operatorname{erf}^{-1}(2p-1)$
Mean	均值	Mean	$\mu$
Median	中位数	Median	$\mu$
Mode	众数	Mode	$\mu$
Variance	方差	Variance	$\sigma^2$
MAD	平均绝对偏差	Median Absolute Deviation	$\sigma \sqrt{2} \operatorname{erf}^{-1}(1 / 2)$
AAD	平均绝对离差	Average Absolute Deviation	$\sigma \sqrt{2 / \pi}$
Skewness	偏度	Skewness	$0$
Excess kurtosis	超额峰度	Excess Kurtosis	$0$
Entropy	熵	Differential Entropy	$\frac{1}{2} \log \left(2 \pi e \sigma^2\right)$
Fisher information	Fisher 信息量	Fisher Information Matrix	$\mathcal{I}(\mu, \sigma) = \begin{pmatrix} \frac{1}{\sigma^2} & 0 \\ 0 & \frac{2}{\sigma^2} \end{pmatrix}$ $\mathcal{I}(\mu, \sigma^2) = \begin{pmatrix} \frac{1}{\sigma^2} & 0 \\ 0 & \frac{1}{2\sigma^4} \end{pmatrix}$
Kullback–Leibler divergence	KL 散度	Kullback–Leibler Divergence	$\frac{1}{2} \left\{ \left(\frac{\sigma_0}{\sigma_1}\right)^2 + \frac{(\mu_1 - \mu_0)^2}{\sigma_1^2} - 1 + \ln \frac{\sigma_1^2}{\sigma_0^2} \right\}$

过程推导

前向过程

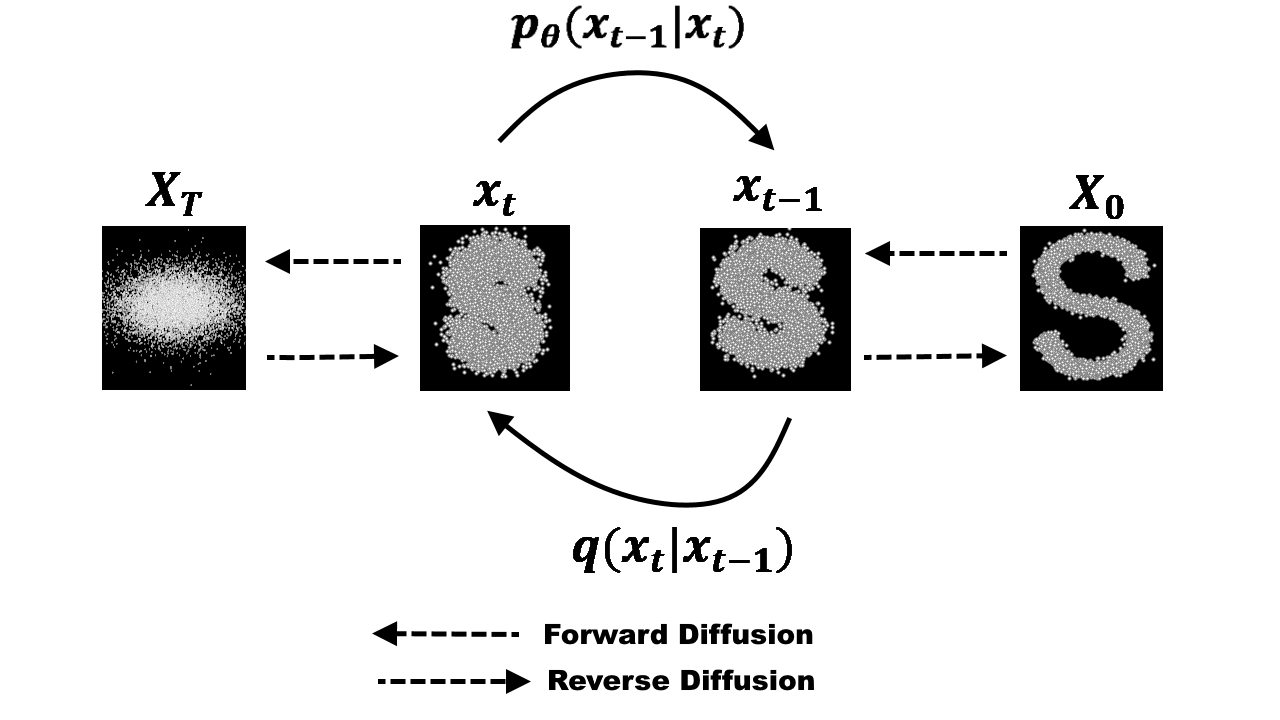
给定真实数据分布为 $\mathbf{x}_0 \sim q(\mathbf{x})$ 采样点，我们定义扩散模型的正向过程（Forward process），其中以步长为增量向样本中添加少量高斯噪声，通过给数据样本 $x_0$ 逐步添加噪声使其生成一系列带有噪音的样本 $\mathbf{x}_{1,},...,\mathbf{x}_T$ ，步长由方差时间表（variance schedule）控制，如式（1）所示，其中 $\left\{\beta_t \in(0,1)\right\}_{t=1}^T$ ：

$$ \mathbf{x}_t=\sqrt{1-\beta_t} \mathbf{x}_{t-1}+\sqrt{\beta_t} \boldsymbol{\epsilon}, \quad \boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \tag{1} $$

该过程可以被定义为一组条件概率序列，由于该过程是马尔可夫链（Markov chain），每个 $x_t$ 仅依赖于前一步的 $x_{t-1}$ ，不直接依赖于 $x_0$ 或者早期步骤：

$$ \begin{split} & q\left(x_1, \ldots, x_T \mid x_0\right)=q\left(x_1 \mid x_0\right) q\left(x_2 \mid x_1, x_0\right) \ldots q\left(x_T \mid x_{T-1}, \ldots, x_0\right) \newline & q\left(x_1, \ldots, x_T \mid x_0\right)=q\left(x_1 \mid x_0\right) q\left(x_2 \mid x_1\right) \ldots q\left(x_T \mid x_{T-1}\right) \end{split} \tag{2} $$

整个的前向过程如下式（3）所示，数据样本 $x_t$ 随着步长 $t$ 的增大，可辨识特征逐渐消失，最终当 $T \rightarrow \infty$ 时， $x_T$ 等价于一个各向同性高斯分布。

$$ q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right):=\prod_{t=1}^T q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right), \quad q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right):=\mathcal{N}\left(\mathbf{x}_t ; \sqrt{1-\beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I}\right) \tag{3} $$

上述过程的一个优点是，我们可以使用重新参数化技巧，以闭合形式在任意时间步长 $t$ 处采样 𝑥𝑡，这里令 $\alpha_t=1-\beta_t$ 和 $\bar{\alpha}_t=\prod_{i=1}^t \alpha_i$ ：

$$ \begin{split} \mathbf{x}_t=\sqrt{\alpha_t} \mathbf{x}_{t-1}+\sqrt{1-\alpha_t} \boldsymbol{\epsilon}_{t-1} \quad; \text { where } \boldsymbol{\epsilon}_{t-1}, \boldsymbol{\epsilon}_{t-2}, \cdots \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \end{split} \tag{4} $$

进一步地

$$ \mathbf{x}_t=\sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2}+\sqrt{1-\alpha_t \alpha_{t-1}} \bar{\epsilon}_{t-2} \quad ; \text { where } \bar{\epsilon}_{t-2} \text { merges two Gaussians }\left(^*\right) \tag{5} $$

最终

$$ \mathbf{x}_t=\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon} \tag{6} $$

因此式（3）变为：

$$ q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)=\mathcal{N}\left(\mathbf{x}_t ; \sqrt{\bar{\alpha}_t} \mathbf{x}_0,\left(1-\bar{\alpha}_t\right) \mathbf{I}\right) \tag{7} $$

(*)当合并两个方差不同的高斯分布时， $\mathcal{N}\left(\mathbf{0}, \sigma_1^2 \mathbf{I}\right)$ 和 $\mathcal{N}\left(\mathbf{0}, \sigma_2^2 \mathbf{I}\right)$ ，新的分布是 $\mathcal{N}\left(\mathbf{0},\left(\sigma_1^2+\sigma_2^2\right) \mathbf{I}\right)$ 。这里的方差应该是 $\sqrt{\left(1-\alpha_t\right)+\alpha_t\left(1-\alpha_{t-1}\right)}=\sqrt{1-\alpha_t \alpha_{t-1}}$ 。通常，当样本噪声增大时，我们可以采用更大的更新步长，因此 $\beta_1<\beta_2<\cdots<\beta_T$ ， $\bar{\alpha}_1>\cdots>\bar{\alpha}_T$ 。

逆向过程

如果我们能够逆转上述过程，并从 $q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)$ 中采样，我们将能够从高斯噪声输入 $\quad \boldsymbol{x_T} \sim (\mathbf{0}, \mathbf{I})$ 中重建真实样本。需要注意的是，如果 $\beta_t$ 足够小， $q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)$ 也将服从高斯分布。遗憾的是，我们无法直接估计 $q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)$ ，因为它需要使用整个数据集，因此我们需要学习一个模型 $p_\theta$ 来近似这些条件概率，以便运行逆向扩散过程。

$$ p_\theta\left(\mathbf{x}_{0: T}\right):=p\left(\mathbf{x}_T\right) \prod_{t=1}^T p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right), \quad p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right):=\mathcal{N}\left(\mathbf{x}_{t-1} ; \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right), \mathbf{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\right) \tag{8} $$

值得注意的是，当条件为 $x_0$ 时，逆条件概率是可计算的：

$$ q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)=\mathcal{N}\left(\mathbf{x}_{t-1} ; \tilde{\boldsymbol{\mu}}\left(\mathbf{x}_t, \mathbf{x}_0\right), \tilde{\beta}_t \mathbf{I}\right) $$

使用贝叶斯法则和高斯概率密度分布函数，可以得到：

$$ \mathcal{N}\left(\mathbf{x} ; \mu, \sigma^2 \mathbf{I}\right) \propto \exp \left(-\frac{1}{2 \sigma^2}\|\mathbf{x}-\mu\|^2\right) $$

$$ \begin{aligned} q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right) & =q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}, \mathbf{x}_0\right) \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)} \\ & \propto \exp \left(-\frac{1}{2}\left(\frac{\left(\mathbf{x}_t-\sqrt{\alpha_t} \mathbf{x}_{t-1}\right)^2}{\beta_t}+\frac{\left(\mathbf{x}_{t-1}-\sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0\right)^2}{1-\bar{\alpha}_{t-1}}-\frac{\left(\mathbf{x}_t-\sqrt{\bar{\alpha}_t} \mathbf{x}_0\right)^2}{1-\bar{\alpha}_t}\right)\right) \\ & =\exp \left(-\frac{1}{2}\left(\frac{\mathbf{x}_t^2-2 \sqrt{\alpha_t} \mathbf{x}_t \mathbf{x}_{t-1}+\alpha_t \mathbf{x}_{t-1}^2}{\beta_t}+\frac{\mathbf{x}_{t-1}^2-2 \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0 \mathbf{x}_{t-1}+\bar{\alpha}_{t-1} \mathbf{x}_0^2}{1-\bar{\alpha}_{t-1}}-\frac{\left(\mathbf{x}_t-\sqrt{\bar{\alpha}_t} \mathbf{x}_0\right)^2}{1-\bar{\alpha}_t}\right)\right) \\ & =\exp \left(-\frac{1}{2}\left(\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}}\right) \mathbf{x}_{t-1}^2-\left(\frac{2 \sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t+\frac{2 \sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} \mathbf{x}_0\right) \mathbf{x}_{t-1}+C\left(\mathbf{x}_t, \mathbf{x}_0\right)\right)\right) \end{aligned} $$

上式可进一步转化为：

$$ \exp \left(-\frac{1}{2}\left[A \cdot \mathbf{x}_{t-1}^2-B \cdot \mathbf{x}_{t-1}+C\left(\mathbf{x}_t, \mathbf{x}_0\right)\right]\right) $$

其中 $C\left(\mathbf{x}_t, \mathbf{x}_0\right)$ 是某个不涉及 $\mathbf{x}_{t-1}$ 的函数，具体细节省略。遵循标准高斯密度函数，根据高斯分布的标准性质，均值就是线性项系数的负值除以二次项系数，高斯分布的方差是二次项系数 A 的倒数，均值和方差可参数化为如下形式（ $\alpha_t=1-\beta_t$ 和 $\bar{\alpha}_t=\prod_{i=1}^t \alpha_i$ ）：

$$ \begin{aligned} \tilde{\beta}_t & =1 /\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}}\right)=1 /\left(\frac{\alpha_t-\bar{\alpha}_t+\beta_t}{\beta_t\left(1-\bar{\alpha}_{t-1}\right)}\right)=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \cdot \beta_t \\ \tilde{\boldsymbol{\mu}}_t\left(\mathbf{x}_t, \mathbf{x}_0\right) & =\left(\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} \mathbf{x}_0\right) /\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}}\right) \\ & =\left(\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} \mathbf{x}_0\right) \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \cdot \beta_t \\ & =\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \mathbf{x}_0 \end{aligned} $$

由于该性质，我们可以将式（6）表示为 $\mathbf{x}_0=\frac{1}{\sqrt{\bar{\alpha}_t}}\left(\mathbf{x}_t-\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t\right)$ 并将它代入上述方程，得到：

$$ \begin{aligned} \tilde{\boldsymbol{\mu}}_t & =\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}}_t}\left(\mathbf{x}_t-\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t\right) \\ & =\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon_t\right) \end{aligned} $$

最大似然估计

方法一

这种设置与变分自编码器（VAE）非常相似，因此我们可以使用变分下界来优化负对数似然函数：

$$ \begin{aligned} -\log p_\theta\left(\mathbf{x}_0\right) & \leq-\log p_\theta\left(\mathbf{x}_0\right)+D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)\right) \\ & =-\log p_\theta\left(\mathbf{x}_0\right)+\mathbb{E}_{\mathbf{x}_{1: T} \sim q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right) / p_\theta\left(\mathbf{x}_0\right)}\right] \\ & =-\log p_\theta\left(\mathbf{x}_0\right)+\mathbb{E}_q\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right)}+\log p_\theta\left(\mathbf{x}_0\right)\right] \\ & =\mathbb{E}_q\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right)}\right] \end{aligned} $$

其中，KL 散度是非负的

$$ \text { Let } L_{\mathrm{VLB}}=\mathbb{E}_{q\left(\mathbf{x}_{0: T}\right)}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right)}\right] \geq-\mathbb{E}_{q\left(\mathbf{x}_0\right)} \log p_\theta\left(\mathbf{x}_0\right) $$

方法二

使用杰森不等式（Jensen’s inequality）同样可以轻松获得它的证据下限（Evidence Lower Bound，ELBO），假设我们希望将交叉熵（cross entropy）作为学习目标进行最小化：

$$ \begin{aligned} L_{\mathrm{CE}} & =-\mathbb{E}_{q\left(\mathbf{x}_0\right)} \log p_\theta\left(\mathbf{x}_0\right) \\ & =-\mathbb{E}_{q\left(\mathbf{x}_0\right)} \log \left(\int p_\theta\left(\mathbf{x}_{0: T}\right) d \mathbf{x}_{1: T}\right) \\ & =-\mathbb{E}_{q\left(\mathbf{x}_0\right)} \log \left(\int q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right) \frac{p_\theta\left(\mathbf{x}_{0: T}\right)}{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)} d \mathbf{x}_{1: T}\right) \\ & =-\mathbb{E}_{q\left(\mathbf{x}_0\right)} \log \left(\mathbb{E}_{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)} \frac{p_\theta\left(\mathbf{x}_{0: T}\right)}{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}\right) \\ & \leq-\mathbb{E}_{q\left(\mathbf{x}_{0: T}\right)} \log \frac{p_\theta\left(\mathbf{x}_{0: T}\right)}{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)} \\ & =\mathbb{E}_{q\left(\mathbf{x}_{0: T}\right)}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right)}\right]=L_{\mathrm{VLB}} \end{aligned} $$

公式简化

为了将方程中的每个项转换为可解析计算的形式，目标函数可以进一步重写为几个 KL 散度和熵项的组合（详见 Sohl-Dickstein 等，2015 年附录 B 中的详细分步过程）：

$$ \begin{aligned} L_{\mathrm{VLB}} & =\mathbb{E}_{q\left(\mathbf{x}_{0: T}\right)}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right)}\right] \\ & =\mathbb{E}_q\left[\log \frac{\prod_{t=1}^T q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)}{p_\theta\left(\mathbf{x}_T\right) \prod_{t=1}^T p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}\right] \\ & =\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=1}^T \log \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}\right] \\ & =\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}\right] \\ & =\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=2}^T \log \left(\frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)} \cdot \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0\right)}\right)+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}\right] \\ & =\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0\right)}+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}\right] \\ & =\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}+\log \frac{q\left(\mathbf{x}_T \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}\right] \\ & =\mathbb{E}_q\left[\log \frac{q\left(\mathbf{x}_T \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_T\right)}+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}-\log p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)\right] \\ & = \mathbb{E}_q[\underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_T \mid \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_T\right)\right)}_{L_T}+\sum_{t=2}^T \underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)\right)}_{L_{t-1}} \underbrace{-\log p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}_{L_0}] \end{aligned} $$

让我们分别标记变分下界损失中的每个部分：

$$ \begin{aligned} L_{\mathrm{VLB}} & =L_T+L_{T-1}+\cdots+L_0 \\ \text { where } L_T & =D_{\mathrm{KL}}\left(q\left(\mathbf{x}_T \mid \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_T\right)\right) \\ L_t & =D_{\mathrm{KL}}\left(q\left(\mathbf{x}_t \mid \mathbf{x}_{t+1}, \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_t \mid \mathbf{x}_{t+1}\right)\right) \text { for } 1 \leq t \leq T-1 \\ L_0 & =-\log p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right) \end{aligned} $$

$L_{\text {VLB }}$ 中的每个 KL 项（除 $L_0$ 外）都比较两个高斯分布，因此它们可以以闭合形式计算。 $L_T$ 是常数，可以在训练过程中忽略，因为 $q$ 没有可学习参数，且 $\mathbf{x}_T$ 是高斯噪声。Ho 等 2020 年模型使用一个独立的离散解码器来表示 $L_0$ ，该解码器由 $\mathcal{N}\left(\mathbf{x}_0 ; \boldsymbol{\mu}_\theta\left(\mathbf{x}_1, 1\right), \boldsymbol{\Sigma}_\theta\left(\mathbf{x}_1, 1\right)\right)$ 派生而来。

KL 散度（Kullback-Leibler divergence ）是一种衡量两个概率分布接近程度的方法，可以想象为概率空间一种距离度量，上式中第一项 $D_{\mathrm{KL}}\left(q\left(\mathbf{x}_T \mid \mathbf{x}_0\right) \| p\left(\mathbf{x}_T\right)\right)$ 不依赖于模型的参数 $\theta$ ，可以忽略，整个模型发现过程有上千步，最后一项表示从到图像 $x_1$ 图像 $x_0$ ，模型已经恢复了绝大部分的图像，因此这一项很小可以忽略，最终只剩下中间项。

$$ \mathbb{E}_q\left[D_{\mathrm{KL}}\left(q\left(\mathbf{x}_T \mid \mathbf{x}_0\right) \| p\left(\mathbf{x}_T\right)\right)+\sum_{t>1} D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)\right)-\log p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)\right] $$

训练损失

我们需要学习一个神经网络来近似逆扩散过程中的条件概率分布， $p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)=\mathcal{N}\left(\mathbf{x}_{t-1} ; \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right), \boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\right)$ 。我们希望训练 $\boldsymbol{\mu}_\theta$ 以预测 $\tilde{\boldsymbol{\mu}}_t=\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_t\right)$ 。由于 $\mathbf{x}_t$ 在训练时可作为输入，因此我们可以重新参数化高斯噪声项，使其预测时间步 $t$ 时输入 $\mathbf{x}_t$ 的 $\boldsymbol{\epsilon}_t$ ：

$$ \begin{aligned} \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right) & =\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon_\theta\left(\mathbf{x}_t, t\right)\right) \\ \text { Thus } \mathbf{x}_{t-1} & =\mathcal{N}\left(\mathbf{x}_{t-1} ; \frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right), \mathbf{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\right) \end{aligned} $$

损失项 $L_t$ 通过参数化来最小化与 $\tilde{\boldsymbol{\mu}}$ 的差异：

$$ \begin{aligned} L_t & =\mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}}\left[\frac{1}{2\left\|\boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\right\|_2^2}\left\|\tilde{\boldsymbol{\mu}}_t\left(\mathbf{x}_t, \mathbf{x}_0\right)-\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)\right\|^2\right] \\ & =\mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}}\left[\frac{1}{2\left\|\boldsymbol{\Sigma}_\theta\right\|_2^2}\left\|\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_t\right)-\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right)\right\|^2\right] \\ & =\mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}}\left[\frac{\left(1-\alpha_t\right)^2}{2 \alpha_t\left(1-\bar{\alpha}_t\right)\left\|\boldsymbol{\Sigma}_\theta\right\|_2^2}\left\|\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right\|^2\right] \\ & =\mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}}\left[\frac{\left(1-\alpha_t\right)^2}{2 \alpha_t\left(1-\bar{\alpha}_t\right)\left\|\boldsymbol{\Sigma}_\theta\right\|_2^2}\left\|\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t, t\right)\right\|^2\right] \end{aligned} $$

重参数化（Reparameterization）

实证研究表明，Ho 等（2020）发现，在训练扩散模型时，采用一个简化的目标函数（忽略权重项）效果更好：

$$ \begin{aligned} L_t^{\text {simple }} & =\mathbb{E}_{t \sim[1, T], \mathbf{x}_0, \epsilon_t}\left[\left\|\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right\|^2\right] \\ & =\mathbb{E}_{t \sim[1, T], \mathbf{x}_0, \epsilon_t}\left[\left\|\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t, t\right)\right\|^2\right] \end{aligned} $$

因此最终损失函数（Final loss function）：

$$ L_{\text {simple }}=L_t^{\text {simple }}+C $$

其中 $C$ 是常数，不依赖于参数 $\theta$

参数 $\beta_t$

在Ho 等（2020）的研究中，前向方差被设置为一个线性递增的常数序列，从 $\beta_1=10^{-4}$ 到 $\beta_T=0.02$ 。与归一化图像像素值的范围 $[-1,1]$ 相比，这些值相对较小。他们在实验中使用的扩散模型虽然生成了高质量的样本，但仍无法达到其他生成模型那样的竞争性模型对数似然值。

Nichol & Dhariwal（2021）提出了几种改进技术，以帮助扩散模型获得更低的负对数似然（NLL）。其中一种改进是使用基于余弦的方差调度方案。调度函数的选择可以任意，只要它在训练过程中提供近线性下降，并在 $t=0$ 和 $t=T$ 附近有细微变化。

$$ \beta_t=\operatorname{clip}\left(1-\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}, 0.999\right) \quad \bar{\alpha}_t=\frac{f(t)}{f(0)} \quad \text { where } f(t)=\cos \left(\frac{t / T+s}{1+s} \cdot \frac{\pi}{2}\right)^2 $$

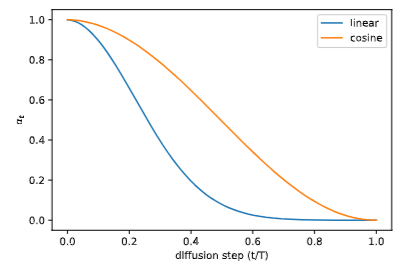
其中，小偏移量 $s$ 用以防止 $\beta_t$ 在接近 $t=0$ 时过小，下图是 $\bar{\alpha}_t$ 在线性时间表和我们提出的余弦时间表中的变化情况。

逆向过程方差 $\boldsymbol{\Sigma}_\theta$ 参数化

Ho 等（2020）选择将 $\beta_t$ 固定为常量而非可学习参数，并设定 $\boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)=\sigma_t^2 \mathbf{I}$ ，其中 $\sigma_t$ 不是学习得到的，而是设置为 $\beta_t$ 或 $\tilde{\beta}_t=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \cdot \beta_t$ 。因为他们发现学习对角方差 $\boldsymbol{\Sigma}_\theta$ 会导致训练不稳定和样本质量较差。

Nichol & Dhariwal (2021) 提出学习 $\boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)$ 作为 $\beta_t$ 和 $\tilde{\beta}_t$ 之间的插值，通过模型预测一个混合向量 $\mathbf{v}$ ：

$$ \boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)=\exp \left(\mathbf{v} \log \beta_t+(1-\mathbf{v}) \log \tilde{\beta}_t\right) $$

然而，简单的目标函数 $L_{\text {simple }}$ 不依赖于 $\boldsymbol{\Sigma}_\theta$ 。为了添加这种依赖性，他们构造了一个混合目标函数 $L_{\text {hybrid }}=L_{\text {simple }}+\lambda L_{\text {VLB }}$ ，其中 $\lambda=0.001$ 是较小的常数，用于在 $L_{\mathrm{VLB}}$ 项中停止梯度对 $\boldsymbol{\mu}_\theta$ 的收敛，确保 $L_{\mathrm{VLB}}$ 仅引导 $\boldsymbol{\Sigma}_\theta$ 的学习。实验中他们观察到 $L_{\text {VLB }}$ 优化难度较大，这可能与梯度噪声有关，因此他们提出使用带重要性采样的 $L_{\mathrm{VLB}}$ 的时间平均平滑版本。

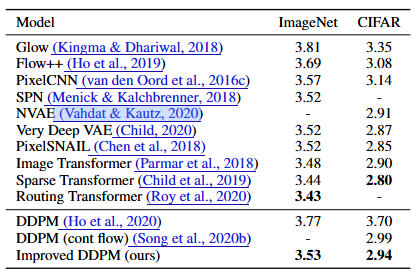
下表是 DDPMs 与其他基于似然度的模型在 CIFAR-10 和无条件 ImageNet $64 \times 64$ 上的比较。非零损失（NLL）以位/维度报告。在 ImageNet $64 \times 64$ 上，我们的模型与最佳卷积模型具有竞争力，但比基于 Transformer 架构的差一些。

条件生成（Conditioned Generation）

在使用包含条件信息的图像数据集（如 ImageNet 数据集）训练生成式模型时，常见的做法是生成基于类标签或一段描述性文本的条件样本。

分类器引导扩散（Classifier Guided Diffusion）

为了显式地将类信息融入扩散过程，Dhariwal 和 Nichol（2021）训练了一个分类器 $f_\phi\left(y \mid \mathbf{x}_t, t\right)$ ，并利用梯度 $\nabla_{\mathbf{x}} \log f_\phi\left(y \mid \mathbf{x}_t\right)$ 引导扩散采样过程向条件信息 $y$ （例如目标类标签）收敛，通过调整噪声预测实现这一目标。回顾一下， $\nabla_{\mathbf{x}_t} \log q\left(\mathbf{x}_t\right)=-\frac{1}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)$ ，我们可以将联合分布 $q\left(\mathbf{x}_t, y\right)$ 的评分函数如下：

$$ \begin{aligned} \nabla_{\mathbf{x}_t} \log q\left(\mathbf{x}_t, y\right) & =\nabla_{\mathbf{x}_t} \log q\left(\mathbf{x}_t\right)+\nabla_{\mathbf{x}_t} \log q\left(y \mid \mathbf{x}_t\right) \\ & \approx-\frac{1}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)+\nabla_{\mathbf{x}_t} \log f_\phi\left(y \mid \mathbf{x}_t\right) \\ & =-\frac{1}{\sqrt{1-\bar{\alpha}_t}}\left(\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)-\sqrt{1-\bar{\alpha}_t} \nabla_{\mathbf{x}_t} \log f_\phi\left(y \mid \mathbf{x}_t\right)\right) \end{aligned} $$

因此，一个新的分类器指导的预测器 $\overline{\boldsymbol{\epsilon}}_\theta$ 将转为如下形式：

$$ \overline{\boldsymbol{\epsilon}}_\theta\left(\mathbf{x}_t, t\right)=\boldsymbol{\epsilon}_\theta\left(x_t, t\right)-\sqrt{1-\bar{\alpha}_t} \nabla_{\mathbf{x}_t} \log f_\phi\left(y \mid \mathbf{x}_t\right) $$

为了控制分类器引导的强度，我们可以添加一个权重 $\boldsymbol{w}$ ，

$$ \overline{\boldsymbol{\epsilon}}_\theta\left(\mathbf{x}_t, t\right)=\boldsymbol{\epsilon}_\theta\left(x_t, t\right)-\sqrt{1-\bar{\alpha}_t} w \nabla_{\mathbf{x}_t} \log f_\phi\left(y \mid \mathbf{x}_t\right) $$

所得的消融扩散模型（ablated diffusion model，ADM）以及带有额外分类器指导的（ADM-G）能够取得比当前最先进生成模型（如 BigGAN）更优的结果。

此外，通过对 U-Net 架构进行一些修改，Dhariwal & Nichol（2021）展示了其性能优于基于扩散模型的生成对抗网络（GAN）。架构修改包括增加模型深度/宽度、增加注意力头数量、多尺度注意力、使用 BigGAN 残差块进行上采样/下采样、通过 $1 / \sqrt{2}$ 进行残差连接缩放，以及自适应组归一化（AdaGN）。

无分类器引导扩散（Classifier-Free Guidance）

在没有独立分类器 $f_\phi$ 的情况下，仍可通过整合条件扩散模型与无条件扩散模型的评分，实现条件扩散步骤（Ho & Salimans, 2021）。令无条件去噪扩散模型 $p_\theta(\mathbf{x})$ 通过分数估计器 $\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)$ 参数化，条件模型 $p_\theta(\mathbf{x} \mid y)$ 通过 $\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t, y\right)$ 参数化。这两个模型可以通过单个神经网络学习。具体来说，条件扩散模型 $p_\theta(\mathbf{x} \mid y)$ 在配对数据 ( $\mathbf{x}, y$ ) 上进行训练，其中条件信息 $y$ 会被随机丢弃，使得模型能够生成无条件图像，即 $\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)=\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t, y=\varnothing\right)$

隐式分类器的梯度可通过条件和无条件分数估计器表示。一旦将这些估计器插入分类器引导的修改后分数中，该分数不再依赖于独立的分类器。

$$ \begin{aligned} \nabla_{\mathbf{x}_t} \log p\left(y \mid \mathbf{x}_t\right) & =\nabla_{\mathbf{x}_t} \log p\left(\mathbf{x}_t \mid y\right)-\nabla_{\mathbf{x}_t} \log p\left(\mathbf{x}_t\right) \\ & =-\frac{1}{\sqrt{1-\bar{\alpha}_t}}\left(\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t, y\right)-\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right) \\ \overline{\boldsymbol{\epsilon}}_\theta\left(\mathbf{x}_t, t, y\right) & =\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t, y\right)-\sqrt{1-\bar{\alpha}_t} w \nabla_{\mathbf{x}_t} \log p\left(y \mid \mathbf{x}_t\right) \\ & =\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t, y\right)+w\left(\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t, y\right)-\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right) \\ & =(w+1) \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t, y\right)-w \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right) \end{aligned} $$

他们的实验表明，无分类器引导方法能够在 FID（区分合成图像与生成图像）和 IS（图像质量与多样性）之间实现良好的平衡。

引导扩散模型 GLIDE（Nichol、Dhariwal & Ramesh 等，2022）探索了两种引导策略：CLIP 引导和无分类器引导，并发现后者更受青睐。他们假设这是因为 CLIP 引导通过利用针对 CLIP 模型的对抗样本来提升模型性能，而非优化生成更匹配的图像。

模型架构

Diffusion Transformer (DiT; Peebles & Xie，2023 ）是一种用于扩散建模的模型，其操作对象为潜在像素块，与潜在扩散模型（LDM）共享相同的潜在空间。DiT 的具体架构如下：

将输入 $\mathbf{z}$ 的潜在表示作为输入传递给 DiT。
将噪声潜在表示（尺寸为 $I \times I \times C$ ）划分为尺寸为 $p$ 的补丁，并将其转换为尺寸为 $(I / p)^2$ 的补丁序列。
然后，这组令牌序列通过 Transformer 块进行处理。他们探索了三种不同的设计，用于在上下文信息（如时间步 $t$ 或类标签 $c$ ）条件下进行生成。在三种设计中，adaLN（自适应层规范）-Zero 表现最佳，优于上下文条件化和交叉注意力块。尺度和偏移参数 $\gamma$ 和 $\beta$ 通过 $t$ 和 $c$ 的嵌入向量之和进行回归。维度缩放参数 $\alpha$ 同样通过回归获得，并在 DiT 块内的残差连接之前立即应用。
Transformer 解码器输出噪声预测和输出对角协方差预测。

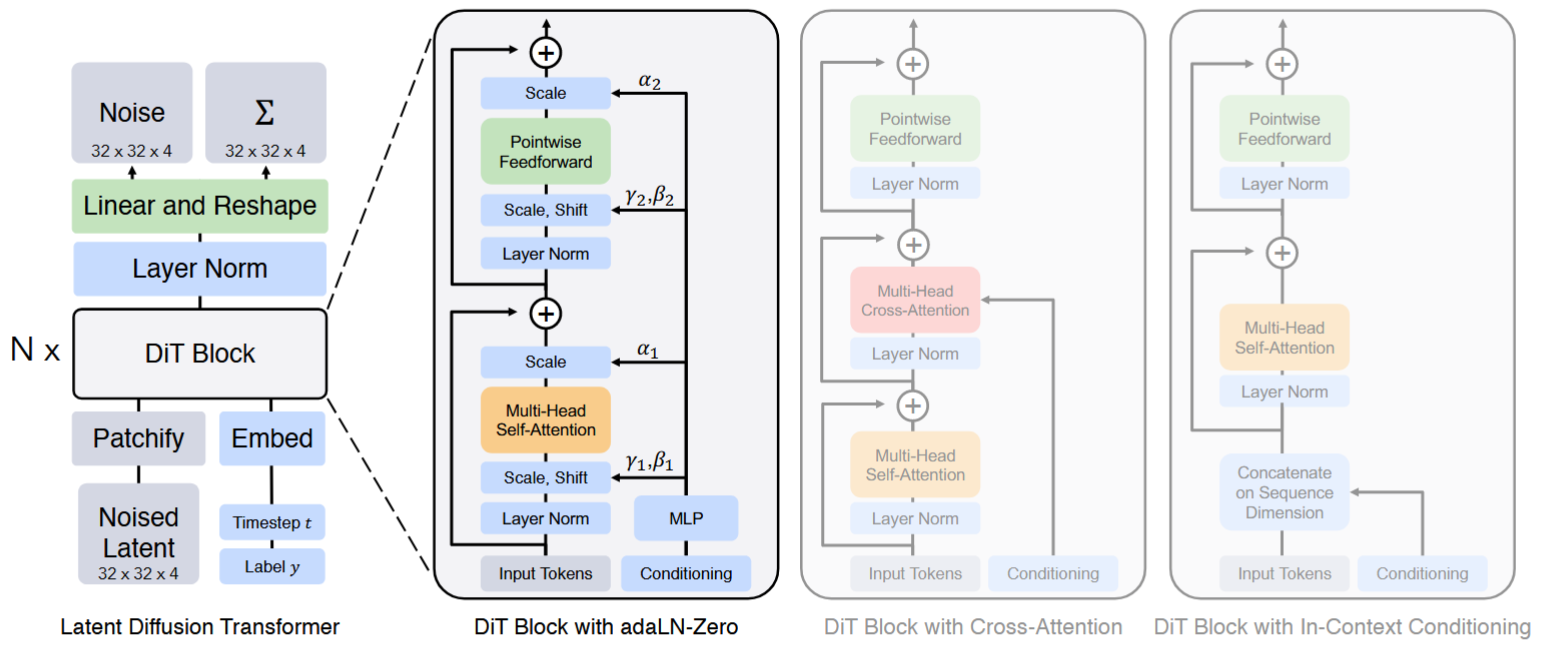
Transformer 架构具有良好的可扩展性，这一点广为人知。这是 DiT 的最大优势之一，因为其性能会随着计算资源的增加而提升，且实验表明，更大的 DiT 模型在计算效率上也更优。

扩散模型（Diffusion models）^[draft]

🗒️ 写在前面

过程推导

前向过程